CHAPTER 3 - Dynamic Programming
3.1 이항 계수 구하기(The Binomial Coefficient)
- 이항계수(Binomial coefficient)는 아래와 같이 정의된다.
$$ \left(\begin{matrix}n\\k\end{matrix}\right)\ =\ \frac{n!}{k!\left(n-k\right)!}\ \ for\ o\ \le \ k\ \le \ n $$
- 값이 큰 n에 대해 n!는 굉장히 큰 수가 되므로, 위의 식으로 이항계수를 구하는 것은 힘들 수 있다.
- 이에 재귀 관계식을 사용하면, n!이나 k!를 계산하지 않고도 이항 계수를 구할 수 있다.
$$ \left(\begin{matrix}n\\k\end{matrix}\right)\ =\ \left(\begin{matrix}n-1\\k-1\end{matrix}\right)\ +\ \left(\begin{matrix}n-1\\k\end{matrix}\right)\ ,\ \ 0<k<n $$
$$ \left(\begin{matrix}n\\k\end{matrix}\right)\ =\ 1\ \ \ \ \ \ \ \ \ \ k=0\ 또는\ k=n $$
- divide and conquer로 이항 계수를 구하는 코드는 아래와 같다.
int bin (int n, int k)
{
if( k == 0 || n == k )
return 1;
else
return bin(n-1, k-1) + bin(n-1, k);
}
- 위의 코드를 실행할 때, 계산하는 항의 개수는 아래와 같다.
$$ 2\left(\begin{matrix}n\\k\end{matrix}\right)\ -\ 1 $$
- 위의 코드는 굉장히 비효율적인데, 그 이유는 재귀 호출할 때마다 같은 사례를 중복 계산하기 때문이다.
(ex) bin(n-1, k-1), bin(n-1, k) 모두 bin(n-2, k-1)의 계산 결과가 필요하다.
- divide and conquer에서 input을 원래 크기와 별 차이 없는 크기로 분할하는 경우이기 때문에 비효율적이다.
- 이에, Dynamic Programming 기법을 사용하여 이항계수를 좀 더 효율적으로 구할 수 있다.
- 이 문제를 푸는 Dynamic Programming의 재귀 관계식은 아래와 같다.
$$ B\left[i\right]\left[j\right]\ =\ \begin{cases}B\left[i-1\right]\left[j-1\right]\ +&B\left[i-1\right]\left[j\right]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0<j<i\\1&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ j\ =\ 0\ 또는\ j\ =\ i\end{cases} $$

- Dynamic Programming으로 이항 계수를 구하는 코드는 아래와 같다.
int bin2 (int n, int k)
{
index i, j;
int B[0..n][0..k];
for(i = 0; i <= n; i++)
for(j = 0; j <= minimum(i, k); j++)
if(j == 0 || j == i)
B[i][j] = 1;
else
B[i][j] = B[i-1][j-1] + B[i-1][j];
return B[n][k];
}
- i 값에 따라 for loop을 도는 횟수는 아래와 같다.

- 이에 총 실행 횟수와 Time Complexity는 아래와 같다. ( (k+1)이 n-k-1 번 더해진다.)
$$ 1\ +\ 2\ +\ 3\ +\ 4\ +\ ...\ +k\ +\ \left(k+1\right)\ +\ \left(k+1\right)+...+\left(k+1\right) $$
$$ \frac{k\left(k+1\right)}{2}\ +\ \left(n-k+1\right)\left(k+1\right)\ =\ \frac{\left(2n-k+2\right)\left(k+1\right)}{2}\in \Theta \left(nk\right) $$
3.2 프로이드의 최단경로 알고리즘(Floyd's Algorithm for Shortest Paths)
- 그래프(Graph)를 그림으로 표현하는 경우, 원은 마디(Vertex), 마디를 잇는 선은 이음선(Edge)이라고 한다.
- 이음선(Edge)에 방향이 있는 그래프는 방향 그래프(Directed Graph, digraph)라고 한다.
- 이음선(Edge)와 관련된 값을 가중치(weights)라고 하며, 가중치가 있는 그래프를 weighted graph라고 한다.
- 방향 그래프(Directed Graph)에서 다음 마디(Vertex)로 가는 이음선(Edge)가 있는 마디(Vetex)의 Sequence를 Path라고 하며,
어떤 마디에서 그 마디 자신으로 가는 경로는 Cycle이라고 한다.
- 그래프에 Cycle이 있으면 cyclic 하다고 하며, 없는 경우에는 acyclic 하다고 한다.
- 같은 마디(Vertex)를 두 번 이상 거치지 않는 경로를 simple path라고 한다.
- weighted graph에서 path의 length는 path 상에 있는 weight들의 합이며, weight가 없는 graph에서는 path 상에서의 이음선(edge)의 개수이다.
- 최단 경로(Shortest Path) 문제는 최적화 문제(Optimization problem)에 속한다.
- 최적화 문제에는 하나 이상의 해답 후보(Candidate solution)이 있을 수 있다.
- 해답 후보에는 그와 관련된 Value가 있고, 해당 문제의 해답은 해답 후보 값들 중 최적값(Optimal value)가 된다.
- vertex A에서 vertex B로 가는 이음선(Edge)가 있는 경우 A는 B에 인접하다(adjacent)
- 인접 행렬(adjacent matrix) W는 아래와 같은 규칙에 따라 작성할 수 있다.
$$ W\left[i\right]\left[j\right]=\begin{cases}weight\ on\ edge\ \ \ \ \ \ A에서\ B로가는\ 이음선이\ 있는\ 경우\\\infty \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A에서\ B로가는\ 이음선이\ 없는\ 경우\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=j인\ \ 경우\end{cases} $$
- 예시로 왼쪽 아래 그림의 Weighted Directed graph는 오른쪽의 adjacent matrix로 나타날 수 있다.
- 최단 경로 문제를 DP(Dynamic Programming)으로 풀기 위해서는 배열 D가 필요하다.
- 배열 D는 아래와 같이 작성된다.
$$ {D}^{\left(k\right)}\left[i\right]\left[j\right]\ =\ set\ \left\{{v}_1\ ,{v}_2\ ,\ ...\ ,\ v_k\ \right\}에속하는\ vertex\ 만을\ 거쳐서\ {v}_i에서\ {v}_j로가는\ shortest\ path $$
- 아래 그림은 weighted directed graph의 배열 W, D를 나타낸 예시이다.

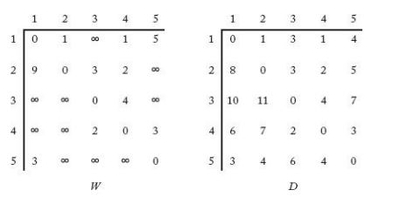
- vertex i에서 vertex j로 가는 최단 경로는, i와 j 사이에 특정 vertex k를 최소한 하나의 vertext가 거치지 않는 경우와 모두 거치는 경우로 나눌 수 있다.
(case 1) vertex i와 j로 가는 최단 경로 중 최소한 하나는 특정 vertex k를 거치지 않는 경우
- vertex k를 거치지 않게 되므로, 아래의 수식이 성립하게 된다.
$$ {D}^{\left(k\right)}\left[i\right]\left[j\right]\ =\ D^{\left(k-1\right)}\left[i\right]\left[j\right] $$
(case 2) vertex i와 j로 가는 최단 경로가 모두 특정 vertex k를 거치는 경우
- vertex k를 무조건 거치므로, shortest_path(i, j) = shortest_path(i, k) + shortest_path(k, j)이다.

- 이에 case2에서는 아래 수식을 만족하게 된다.
$$ {D}^{\left(k\right)}\left[i\right]\left[j\right]\ =\ D^{\left(k-1\right)}\left[i\right]\left[k\right]\ +\ {D}^{\left(k-1\right)}\left[k\right]\left[j\right] $$
- 최종적으로 배열 D를 구하는 수식은 아래와 같다. (min의 첫 번째 항은 case 1, 두 번째 항은 case 2)
$$ D^{\left(k\right)}\left[i\right]\left[j\right]\ \ =\ \min _{ }^{ }\left({D}^{\left(k-1\right)}\left[i\right]\left[j\right],\ \ \ {D}^{k-1}\left[i\right]\left[k\right]\ +\ {D}^{k-1}\left[k\right]\left[j\right]\right) $$
- Floyd의 Shortest Path Algorithm code는 아래와 같다.
void floyd (int n, const number W[][], number D[][])
{
index i, j, k;
D = W;
for(k = 1; k <= n; k++)
for(i = 1; i <= n; i++)
for(j = 1; j <= n; j++)
D[i][j] = minimum(D[i][j], D[i][k] + D[k][j]);
}
- 위의 코드는 for-loop 3개가 n 번씩 돌게 되므로, 시간 복잡도 T(n)은 아래와 같이 계산된다.
$$ T\left(n\right)\ =\ n\ \times n\times n={n}^3\ \in \Theta \left({n}^3\right) $$
3.3 동적 계획과 최적화 (Dynamic Programming and Optimizaiton Problems)
- 최적화 문제를 동적계획법(Dynamic Programming)으로 풀기 위해서는 최적의 원칙이 성립해야 한다.
- 어떤 문제의 입력 사례(instance)가 그 입력 사례를 분할한 부분 사례(substances)에 대한 optimal solution을
항상 포함하고 있으면, 해당 문제는 최적의 원칙(Principle of optimality)이 성립한다고 한다.
- 최적의 원칙이 성립하지 않는 예시로는, 최장 경로 문제(Longest path problem)이 있다.
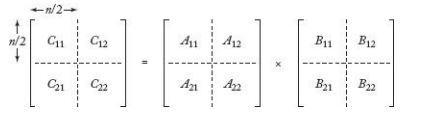
3.4 연쇄 행렬 곱셈 (Chained Matrix Multiplication)
- (i * j) 행렬과 (j * k) 행렬을 곱하면 원소 단위 곱셈의 실행횟수는 (i * j * k) 번이 된다.
- 6개의 행렬을 곱하는 최적의 순서는 다음의 5개 경우 중 하나이다.
$$ 1.\ {A}_1\left({A}_2{A}_3{A}_4{A}_5{A}_6\right) $$
$$ 2.\ \left({A}_1{A}_2\right)\left({A}_3{A}_4{A}_5{A}_6\right) $$
$$ 3.\ \left({A}_1{A}_2{A}_3\right)\left({A}_4{A}_5{A}_6\right) $$
$$ 4.\ \left({A}_1{A}_2{A}_3{A}_4\right)\left({A}_5{A}_6\right) $$
$$ 5.\left(\ {A}_1{A}_2{A}_3{A}_4{A}_5\right){A}_6 $$
- 행렬 M을 아래와 같이 정의할 때,
$$ M\left[i\right]\left[j\right]\ =\ i<\ j\ 일때,\ {A}_i부터\ {A}_j까지\ 행렬을곱하는데\ 필요한원소단위\ 곱셈의최소\ 횟수 $$
$$ M\left[i\right]\left[i\right]\ =0 $$
재귀 관계식은 아래와 같이 나타난다.
$$ M\left[i\right]\left[j\right]\ =\ \min _{i\ \le \ k\ \le \ j-1}^{ }\left(M\left[i\right]\left[k\right]\ +\ M\left[k+1\right]\left[j\right]\ +\ {d}_{i-1}{d}_k{d}_j\right),\ \ \ \ \ \ \ \ \ \ if\ \ i\ <\ j $$
$$ M\left[i\right]\left[i\right]\ =\ 0 $$
- 위의 관계식을 기반으로 하여 divide and conquer 기법을 사용하면 지수 시간 알고리즘에 해당한다.
- 이에 아래 그림과 같이 dynamic programming을 사용하여 좀 더 효율적으로 알고리즘을 작성할 수 있다.
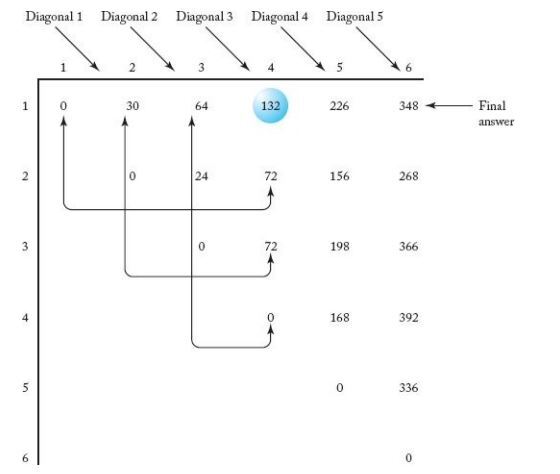
- 최소 곱셈의 코드는 아래와 같다.
int minmult (int n, const int d[], index P[][])
{
index i, j, k, diagonal;
int M[1..n][1..n];
for(i = 1; i <= n; i++)
M[i][i] = 0;
for(diagonal = 1; diagonal <= n-1; diagonal++){
for(i = 1; i <= n-diagonal; i++){
j = i + diagonal;
for(k = i; k <= j-1; k++){
M[i][j] = minimum(M[i][k] + M[k+1][j] + d[i-1] * d[k] * d[j]);
P[i][j] = a value of k that gave the minimum;
}
}
}
return M[1][n];
}
- 최소 곱셈의 시간 복잡도는 아래와 같다.
- (j = i + diagonal)이므로, k-loop 안에서 실행되는 횟수는 아래와 같다.
$$ \left(j-1\right)\ -\ i\ \ +\ 1\ =\ \left(i+diagonal-1\right)\ -\ i\ +\ 1\ =\ diagonal $$
- 주어진 diagonal 값에 대해서 i-loop에서 실행하는 횟수는 n-diagonal이 되고, diagonal 값은 1~(n-1)이므로
$$ \sum _{diaognal=1}^{n-1}\left[\left(n-diagonal\right)\ \times diagonal\right]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{n\left(n-1\right)\left(n+1\right)}{6}\in \Theta \left(n^3\right) $$
3.5 최적 이분 검색 트리(Optimal Binary Search Trees)
- 이분 검색 트리(Binary Search Tree)의 원소들을 최적으로 정리하는 알고리즘을 만들어보자.
- 이진 트리(Binary)에서 어떤 마디(node)의 왼쪽[오른쪽] 자식 마디(child)를 root로 하는 하위 트리를
그 마디의 왼쪽 하위 트리(Left Subtree)[오른쪽 하위 트리(Right Subtree)]라고 한다.
* 정의
- 이분 검색 트리(Binary Search Tree)는 Ordered set으로 속한 원소로 구성된 이진 트리(Binary Tree)이다.
- 이분 검색 트리는 아래와 같은 조건을 만족한다.
(1) 각 마디(node)는 하나의 원소(element)만을 가지고 있다.
(2) 마디의 왼쪽 하위 트리에 있는 원소들은 모두 그 마디의 원소보다 작거나 같다.
(3) 마디의 오른쪽 하위 트리에 있는 원소들은 모두 그 마디의 원소보다 크거나 같다.
- 마디의 깊이(Depth of node)는 root에서 해당 node로 가는 unique path에서 edge의 개수이다.
- 트리의 깊이(Depth of tree)는 해당 트리의 모든 마디의 깊이 중 최댓값을 나타낸다.
- 깊이(Depth)는 때때로 수준(Level)이라고도 불린다.
- 모든 마디의 두 하위 트리의 깊이가 1 이상 차이 나지 않는 트리를 balanced Tree라고 한다.
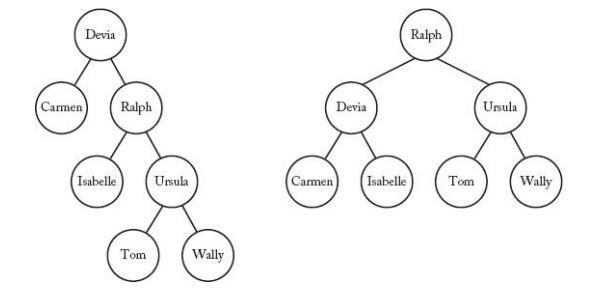
- 위 그림의 왼쪽 Tree는 Balanced Tree가 아니며, 오른쪽 Tree는 Balanced Tree이다.
- Binary Search Tree에서 search key를 찾는 데 걸리는 평균 시간이 최소가 되도록 정리하는 것이 중요하며,
그렇게 정리한 Tree를 최적(Optimal)이라고 한다.
- 만약 각 원소가 search key 일 확률이 모두 같다고 하면, 오른쪽 Tree는 Optimal이다.
- Binary Search Tree에서 원소를 검색하는 코드는 아래와 같다.
struct nodetype
{
keytype key;
nodetype* left;
nodetype* right;
}
typedef nodetype* node_pointer;
void search (node_pointer tree, keytype keyin, node_pointer& p) // keyin : search key
{
bool found;
p = tree;
found = false;
while(!found){
if(p->key == keyin)
found = true;
else if(keyin < p->key)
p = p->left;
else if(keyin > p->key)
p = p->right;
}
}
- 최적 트리는 해당 트리의 left sub-tree의 최적 트리와 right sub-tree의 최적 트리를 포함한다.
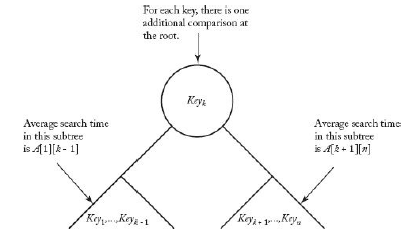
- 트리 k에 대한 평균 검색 시간은 아래와 같다.
$$ A\left[1\right]\left[k-1\right]\ +\left(\ {p}_1\ +\ ...\ +\ {p}_{k-1}\right)\ +\ {p}_k\ +\ A\left[k+1\right]\left[n\right]\ +\left(\ {p}_{k+1}\ +\ ...\ +\ {p}_n\right)\ $$
A[1][k-1] : left sub-tree에서의 평균 시간
p(1) + ... + p(k-1), p(k+1) ... + p(n) : 뿌리에서 비교하는데 드는 추가시간
p(k) : 뿌리를 검색하는 평균 시간
A[k+1][n] : right sub-tree에서의 평균 시간
- 위의 식을 정리하면 아래와 같다.
$$ A\left[1\right]\left[k-1\right]\ +\ A\left[k+1\right]\left[n\right]\ +\ \sum _{m=1}^n{p}_m $$
$$ A\left[1\right]\left[n\right]\ =\ \min _{1\le k\le n}^{ }\left(A\left[1\right]\left[k-1\right]+A\left[k+1\right]\left[n\right]\right)\ +\ \sum _{m=1}^n{p}_m\ $$
- 따라서 일반식으로 정리하면 아래와 같다.
$$ A\left[i\right]\left[j\right]\ =\ \min _{i\le k\le j}^{ }\left(A\left[i\right]\left[k-1\right]+A\left[k+1\right]\left[j\right]\right)\ +\ \sum _{m=i}^j{p}_m\ \ ,\ i<j $$
$$ A\left[i\right]\left[i\right]\ =\ {p}_i $$
$$ A\left[i\right]\left[i-1\right]\ =\ 0 $$
$$ A\left[j+1\right]\left[j\right]\ =\ 0 $$
- 최적 이분 검색 트리 (Optimal Binary Serach Tree)에 대한 코드는 아래와 같다.
void optsearchtree(int n, const float p[], float& minavg, index R[][])
{
index i, j, k, diagonal;
float A[1 .. n+1][0 .. n];
for(i=1; i<=n; i++){
A[i][i-1] = 0;
A[i][i] = p[i];
R[i][i] = i;
R[i][i-1] = 0;
}
A[n+1][n] = 0;
R[n+1][n] = 0;
for(diagonal=1; diagonal<=n-1; diagonal++){
for(i=1; i<=n-diagonal; i++) {
j = i + diagonal;
for(k=i; k<=j; k++){
if(A[i][j] > A[i][k-1] + A[k+1][j]){
A[i][j] = A[i][k-1] + A[k+1][j];
R[i][j] = k;
}
for(m=i; m<=j; m++)
A[i][j] += p[m];
}
}
minavg = A[1][n];
}
- 최적 이분 검색 트리 (Optimal Binary Serach Tree)에 대한 시간 복잡도는 아래와 같다.
$$ T\left(n\right)\ =\ \frac{n\left(n-1\right)\left(n+4\right)}{6}\in \Theta \left(n^3\right) $$
- 최적 이분 검색 트리(Optimal Binary Search Tree)를 구축하는 코드는 아래와 같다.
node_pointer tree (index i, j)
{
index k;
node_pointer p;
k = R[i][j];
if(k == 0)
return NULL;
else {
p = new_nodetype;
p->key = Key[k];
p->left = tree(i, k-1);
p->right = tree(k+1, j);
return p;
}
}3.6 외판원 문제(The Traveling Salesperson Problem)
- 외판원이 20개 도시로 판매 출장을 계획하고 있으며, 각 도시는 몇 개의 도시와 도로로 연결되어 있다.
- 외판원이 자신이 거주하고 있는 도시에서 출발하여 각 도시를 한 번씩 방문한 뒤, 다시 출발한 도시로 돌아오는
여행길을 찾는 문제를 외판원 문제(The Traveling Salesperson problem)이라고 한다.
- 이 문제는 도시를 마디(vertex, node)로 하여 weighted directed graph로 표현하여 문제를 해결할 수 있다.
- 일주여행길(tour)는 해밀턴 회로(Hamiltonian circuits)라고도 하며, optimal tour는 최소 거리 tour이다.
- n 개의 도시가 있고 각 도시에서 다른 도시로의 edge가 모두 존재할 때, tour의 총 가지 수는 아래와 같다.
$$ \left(n-1\right)\left(n-2\right)...1\ =\ \left(n-1\right)! $$
- 그래프가 왼쪽 아래와 같이 있을 때, 인접 행렬(adjacent matrix) W는 오른쪽 아래와 같이 나타난다.
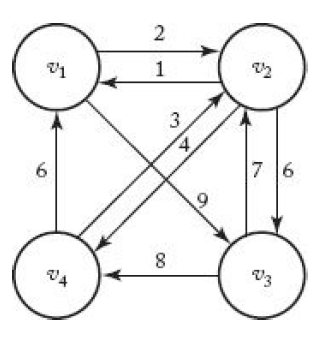
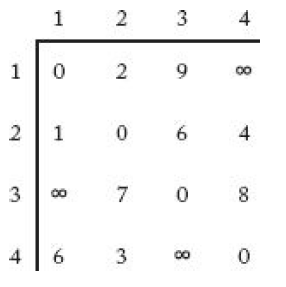
- 이 문제에서 사용할 변수는 아래와 같다.
V = 모든 도시의 집합 , A = V의 부분집합
D[v(i)][A] = A에 속한 도시를 각각 한 번씩만 거쳐서 v(i)에서 v(1)로 가는 최단 경로의 길이
이때, optimal tour의 길이는 아래와 같다.
$$ \min _{2\le j\le n}^{ }\left(W\left[1\right]\left[j\right]\ +\ D\left[{v}_j\right]\left[V-\left\{v_1,\ v_j\right\}\right]\right) $$
- 이를 구현한 코드는 아래와 같다.
void travel(int n, const number W[][], index P[][], number& minlength)
{
index i, j, k;
number D[1..n][subnet of V-{v(1)}];
for(i=2; i<=n; i++)
D[i][empty] = W[i][1];
for(k=1; k<=n-2; k++){
for(all subnet A containing k vertices){
for(i such that i!= 1 and v(i) is not in A){
D[i][A] = min(W[i][j] + D[i][A - {v(j)}]);
P[i][A] = value of j that gave the minimum;
}
}
}
D[1][V - {v(1)}] = min(W[1][j] + D[j][V-{v(1), v(j)}]);
P[1][V - {v(1)}] = value of j taht gave the minimum;
min length = D[1][V - {v(1)});
}
- 외판원 문제의 시간 복잡도와 공간 복잡도는 아래와 같다.
$$ T\left(n\right)\ =\ \sum _{k=1}^{n-2}\left(n-1-k\right)k\left(\begin{matrix}n-1\\k\end{matrix}\right)\ =\ \left(n-1\right)\left(n-2\right){2}^{n-3}\in \Theta \left(n^22^n\right) $$
$$ M\left(n\right)\ =\ 2\ \times n2^{n-1}\ =\ n2^n\ \in \Theta \left(n2^n\right) $$
- 최악 시간 복잡도(Worst-case Time Complexity)가 지수 시간보다 좋은 외판원 문제를 푸는 알고리즘은 없다.
- 하지만, 지수 시간보다 좋은 알고리즘이 없다고 증명한 사람도 존재하지 않는다.
3.7 DNA 서열 정렬(Sequence Alignment)
- DNA는 A, G, C, T 4개의 염기로 구성되어 있으며, (A, T)와 (G, C)가 쌍을 이룬다.
- 동족서열이 아래와 같을 때,
A A C A G T T A C C
T A A G G T C A
틈(gap)의 cost를 1, 불일치(mismatch)의 cost를 3으로 두면,
_ A A C A G T T A C C
T A A _ G G T _ _ C A
인 경우에는 정렬에 드는 cost가 10(1 + 1 + 3 + 1 + 1 + 3)이다.
A A C A G T T A C C
T A _ A G G T _ C A
인 경우에는 정렬에 드는 cost가 11(3 + 1 + 3 + 1 + 3)이다.
- 최적 정렬(Optimal alignment)를 구하기 위한 계산은 아래 3가지 경우 중 하나로 시작해야 한다.
(1) x[0]과 y[0]을 맞추어 정렬한다. x[0] = y[0]이면, 첫 alignment site에서는 peantly가 없고,
x[0] != y[0]이면 penalty가 1이다.
(2) x[0]과 gap을 맞추어 정렬하고, 첫 alignment site에서 peanlty가 2이다.
(3) y[0]과 gap을 맞추어 정렬하고, 첫 alignment site에서 penalty가 2이다.
- DNA 서열 정렬을 위해 divide and conquer 방법을 사용하면 코드는 아래와 같다.
void opt (int i, int j)
{
if( i == m )
opt = 2(n - j);
else if( j == n )
opt = 2(m - i);
else {
if(x[i] == y[j])
penalty = 0;
else
penalty = 1;
opt = min(opt(i + 1, j + 1) + penalty, opt(i + 1, j) + 2, opt(i , j + 1) + 2);
}
}
- 위의 divide and conquer 방법을 사용하면 중복 계산되는 항들이 많아지게 되어 비효율적이게 된다.
- 이에 배열을 사용하여 아래와 같이 구해볼 수 있다.
- Diagonal1, Diagonal2, ... 로 계산을 수행해가며, 최종 답인 cost 값은 [0][0]에 저장되게 된다.
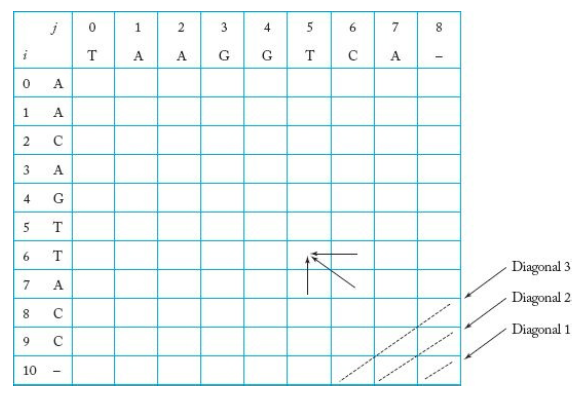
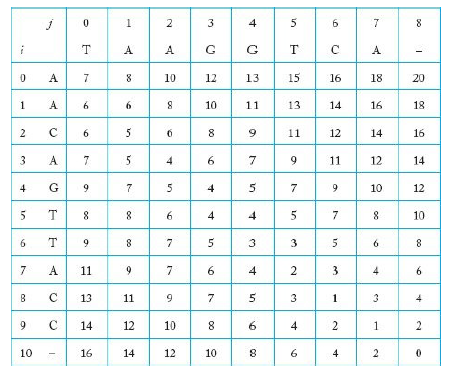
- 위 배열에서 어떻게 [0][0] 값을 계산했는지 경로를 추적할 수 있다.
(1) [0][0]을 선택한다.
(2) 경로에 넣을 둘째 항목을 찾는다.
(a) [0][1]을 검사한다. (b) [1][0]을 검사한다. (c) [1][1]을 검사한다.
- 경로를 찾으면, 정렬된 서열(alignmented sequence)를 다음과 같이 추출할 수 있다.
(1) 배열의 오른쪽 맨 아래부터 시작하여 표시해둔 경로를 따라간다.
(2) 배열의 [i][j] 칸에 도달하기 위해서 대각선으로 이동할 때마다, i 번째 항에 해당하는 문자를 x에 넣고, j 번째 열에 해당하는 문자를 y 서열에 넣는다.
(3) 배열의 [i][j] 칸에 도달하기 위해서 위로 이동할 때마다, i 번째 항에 해당하는 문자를 x 서열에 넣고, 틈 문자(gap)을 y 서열에 넣는다.
(4) 배열의 [i][j] 칸에 도달하기 위해서 왼쪽으로 이동할 때마다, j 번째 행에 해당하는 문자를 y 서열에 넣고, 틈 문자(gap)을 x 서열에 넣는다.
-Reference-
Neapolitan, Richard E., 『Foundation of algorithms FIFTH EDITION』
'알고리즘 > 학부수업 이론' 카테고리의 다른 글
| Foundation of Algorithm - CHAPTER 2 (0) | 2022.05.08 |
|---|---|
| Foundation of Algorithm - CHAPTER 1 (0) | 2022.05.08 |